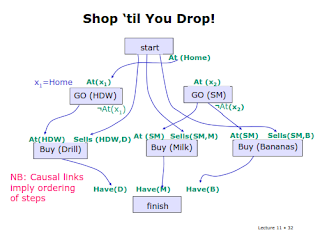
Graph Plan adalah algoritma yang digunakan untuk perencanaan
otomatis yang dikembangkan oleh Avrim Blum dan Merrick Furst pada tahun 1995.
Graph Plan mengambil input masalah perencanaan
yang dinyatakan dalam strip, dan mengerjakan jika salah satu memungkinkan untuk
urutan operasi guna mencapai keadaan goal state.
Didalam Graph Plan terdapat constrain yang disebut dengan
Mutually Exclusive Action atau Mutex. Mutex dapat diartikan jika dua tindakan tidak dapat dikerjakan secara paralel. Hubungan mutex sangat
bervariasi dari lapisan ke lapisan, jadi kita akan memiliki pertanyaan mengenai kapan dua tindakan yang mutex di
tingkat i. Hal ini dapat menjadi kenyataan dalam tiga kondisi yang
memungkinkan.
Selain itu terdapat juga mutex yang lain seperti gambar dibawah ini.
Contoh pengaplikasian Graph Plan : Birthday Dinner
Example
Berikut adalah initial
state, goal state, dan aksi-aksi yang dapat kita lakukan :
Diawali dengan meletakkan initial state nya.
Selanjutnya kita akan memasukkan aksi yang dapat dilakukan dan
hubungkan dengan initial state.
Setelah itu kita masukkan hasil dari setiap aksi
yang bisa kita lakukan.
Karena sekarang kita telah membuat dasar dalam Graph Plan.
Selanjutnya yang harus dilakukan adalah membuat Mutex dari Graph Plan ini. Alasan pertama bahwa
tindakan dapat mutex adalah karena efek yang tidak konsisten. Jadi, clean mutex
dengan carry, karena carry membuat clean menjadi salah. Begitu pula dengan garbage
mutex dengan carry dan dolly karena carry dan dolly membuat garbage salah.
Quite juga mendapatkan efek yang sama dengan dolly karena dolly membuat quite
menjadi salah.
Alasan lain mutex dapat terjadi adalah karena adanya
gangguan seperti suatu aksi yang meniadakan prekondisi dari aksi yang lain. Carry Mutex
dengan cook karena hasil dari carry meniadakan prekondisi dari cook. Dolly
mutex wrap karena hasil dari dolly meniadakan prekondisi dari wrap. Selanjutnya
carry dan dolly mutex karena mereka saling meniadakan prekondisi mereka.
Selanjutnya, setiap preposisi mutex dengan negasi nya.
Lalu, alasan lain yang mana kita mungkin memiliki mutex adalah karena dukungan yang tidak konsisten. Jadi, garbage mutex dengan not clean
dan not quite karena untuk mendapatkan garbage kita harus membiarkan nya dan
ini mutex dengan carry dan dolly. Dinner mutex dengan not clean karena cook dan
carry mutex pada level sebelumnya. Present mutex dengan not quite karena warp
dan dolly mutex pada level sebelumnya. Begitupula dengan not clean dan not
quite karena carry dan dolly mutex pada level sebelumnya. Itulah mutex yang
bisa kita dapatkan.
Setelah itu kita mulai untuk mendapatkan goals yang kita butuhkan. Pertama-tama kita akan
mendapatkan not garbage, kita menggunakan aksi carry, lalu kita mencoba
mendapatkan dinner dengan aksi cook satu satunya aksi untuk mendapatkan dinner.
Tetapi cook dan carry adalah mutex jadi kita tidak dapat menggunakan aksi
tersebut.
Lalu kita coba dengan menggunakan cara lain, yaitu kita akan
mendapatkan not garbage dengan aksi dolly, lalu kita dapat mendapatkan dinner
menggunakan cook, tetapi kita tidak dapat mendapatkan present dengan satu-satu
nya cara mendapatkan present yaitu warp, karena warp dengan dolly merupakan
mutex.
Ternyata kita tidak bisa mendapatkan goal dengan cara ini.
Untuk itu kita akan menggunakan depth two plan. Yaitu dengan menambahkan dua level
lagi pada graph.
Nah pada aksi ini kita mendapatkan mutex sama seperti
level sebelumnya.
Selanjutnya pada level ini kita juga akan mendapatkan mutex
seperti pada level sebelumnya. Akan tetapi ada sedikit perbedaan mencolok mutex disini dengan yang ada
di level sebelumnya. Yaitu pada level ini dinner tidak mutex dengan carry karena kita
bisa mendapatkan dinner dengan membiarkan nya dan tetap bisa melakukan carry.
Begitupun dengan present yang tidak mutex dengan dolly karena kita bisa mendapatkan
present dengan membiarkan nya dan dapat tetap melakukan dolly.
Setelah kita selesai dengan mutex, selanjutnya kita coba mencari
lagi apa yang kita butuhkan dan akhirnya kita berhasil dengan melakukan dengan cara sebagai berikut.
Selesai sudah langkah-langkah dalam pengaplikasian Graph Plan. Sekian dan terimakasih, semoga dapat bermanfaat bagi kalian, saya pribadi, dan kita semua...
Sumber referensi :
- https://en.wikipedia.org/wiki/GraphPlan
- Semua gambar diambil dari PDF "Lecture 12 FinalPart1 (Graph Plan)"
- https://ihzhadamy.blogspot.co.id/2016/10/graph-plan.html